Quantum Safe Storage Algoritm

The Quantum Safe Storage Algorithm is the heart of the Storage engine. The storage engine takes the original data objects and creates data part descriptions that it stores over many virtual storage devices (ZDB/s).

Data gets stored over multiple ZDB's in such a way that data can never be lost.

Unique features

• Data always append, can never be lost
• Even a quantum computer cannot decrypt the data
• Data is spread over multiple sites. If these sites are lost the data will still be available
• Protects from datarot

The Problem

Today we produce more data than ever before. We cannot continue to make full copies of data to make sure it is stored reliably. This will simply not scale. We need to move from securing the whole dataset to securing all the objects that make up a dataset.

We are using technology which was originally used for communication in space.

The algo stores data fragments over multiple devices (physical storage devices ).

The solution is not based on replication or sharding, the algo represents the data as equasions which are distributed over multiple locations.

How Data Is Stored Today

In most distributed systems, as used on the Internet or in blockchain today, the data will get replicated (sometimes after sharding, which means distributed based on the content of the file and spread out over the world).

This leads to a lot of overhead and minimal control where the data is.

In well optimized systems overhead will be 400% but in some it can be orders of magnitude higher to get to a reasonable redundancy level.

The Quantum Safe Storage System Works Differently

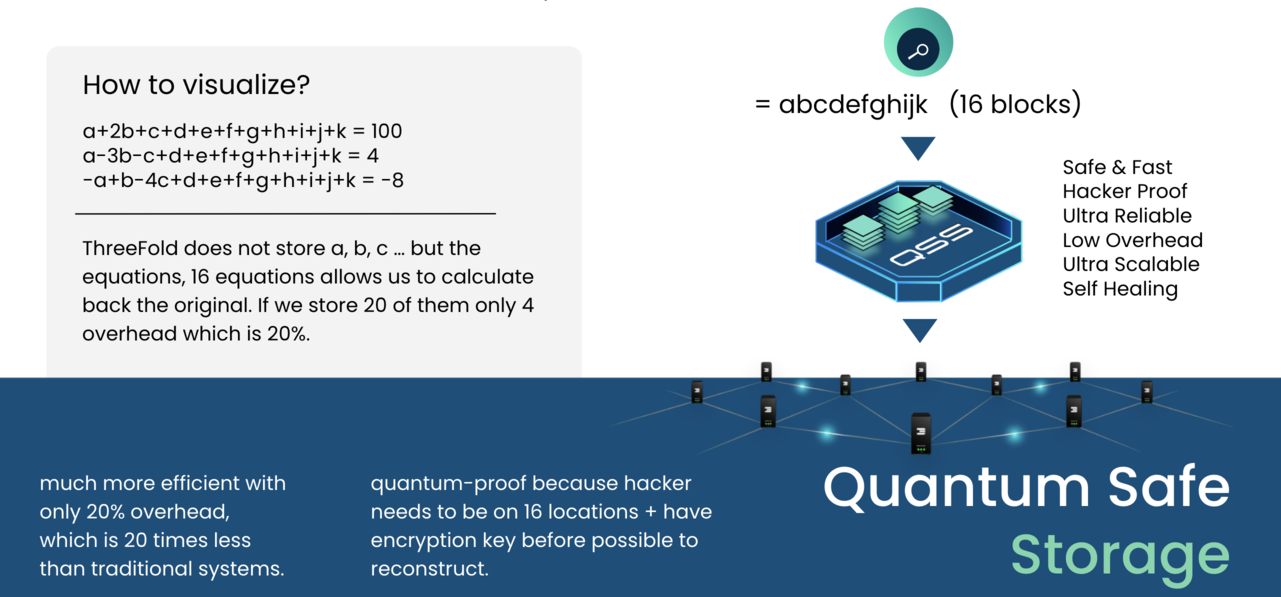
We have developed a new storage algorithm which is more efficient, ultra reliable and gives you full control over where your data is stored.

Our approach is different. Let's try to visualize this new approach with a simple analogy using equations.

Let a,b,c,d.... be the parts of the original object. You could create endless unique equations using these parts. A simple example: let's assume we have 3 parts of original objects that have the following values:

a=1
b=2
c=3

(and for reference the part of the real-world objects is not a simple number like '1' but a unique digital number describing the part, like the binary code for it '110101011101011101010111101110111100001010101111011.....').

With these numbers we could create endless amounts of equations:

1: a+b+c=6
2: c-b-a=0
3: b-c+a=0
4: 2b+a-c=2
5: 5c-b-a=12

etc.

Mathematically we only need 3 to describe the content (value) of the fragments. But creating more adds reliability. Now store those equations distributed (one equation per physical storage device) and forget the original object. So we no longer have access to the values of a, b, c and we just remember the locations of all the equations created with the original data fragments.

Mathematically we need three equations (any 3 of the total) to recover the original values for a, b or c. So do a request to retrieve 3 of the many equations and the first 3 to arrive are good enough to recalculate the original values. Three randomly retrieved equations are:

5c-b-a=12
b-c+a=0
2b+a-c=2

And this is a mathematical system we could solve:

• First: 'b-c+a=0 -> b=c-a'
• Second: '2b+a-c=2 -> c=2b+a-2 -> c=2(c-a)+a-2 -> c=2c-2a+a-2 -> c=a+2'
• Third: '5c-b-a=12 -> 5(a+2)-(c-a)-a=12 -> 5a+10-(a+2)+a-a=12 -> 5a-a-2=2 -> 4a=4 -> a=1'

Now that we know 'a=1' we could solve the rest 'c=a+2=3' and 'b=c-a=2'. And we have from 3 random equations regenerated the original fragments and could now recreate the original object.

The redundancy and reliability in this system results from creating equations (more than needed) and storing them. As shown these equations in any random order can recreate the original fragments and therefore redundancy comes in at a much lower overhead.

In our system we don't do this with 3 parts but with thousands.

Example of 16/4

Each object is fragmented into 16 parts. So we have 16 original fragments for which we need 16 equations to mathematically describe them. Now let's make 20 equations and store them dispersedly on 20 devices. To recreate the original object we only need 16 equations. The first 16 that we find and collect allows us to recover the fragment and in the end the original object. We could lose any 4 of those original 20 equations.

The likelihood of losing 4 independent, dispersed storage devices at the same time is very low. Since we have continuous monitoring of all of the stored equations, we could create additional equations immediately when one of them is missing, making it an auto-regeneration of lost data and a self-repairing storage system.

The overhead in this example is 4 out of 20 which is a mere 20% instead of 400% .

Content Delivery

This system can be used as backend for content delivery networks.

E.g. content distribution policy could be a 10/50 distribution which means, the content of a movie would be distributed over 60 locations from which we can lose 50 at the same time.

If someone now wants to download the data, the first 10 locations to answer will provide enough of the data parts to rebuild the data.

The overhead here is more, compared to previous example, but stil orders of magnitude lower compared to other CDN systems.

The Quantum Safe Storage System Can Avoid Datarot

Datarot is the fact that data storage degrades over time and becomes unreadable e.g. on a harddisk.

The storage system provided by ThreeFold intercepts this silent data corruption ensurinf that data does not rot.

See also https://en.wikipedia.org/wiki/Data_degradation